In this post, I give a proof of the convergence of gradient descent for the class of convex functions with Lipschitz continuous gradient. Then, I show that the convergence rate of gradient descent can be improved by simply adding an momentum (extrapolation) step. The proofs in this post are adapted from the paper A Fast Iterative Shrinkage-Thresholding Algorithm for Linear Inverse Problems.
Preliminaries
Definition 1. A differentiable function $f : \mathbb{R}^d \rightarrow \mathbb{R}$ is convex if
\begin{aligned} f(x) \geq f(y) + \langle \nabla f(y), x - y \rangle \end{aligned}
for any $x, y \in \mathbb{R}^d$. This means that $f$ lies above its tangent hyperplanes.
Definition 2. A differentiable function $f : \mathbb{R}^d \rightarrow \mathbb{R}$ has a Lipschitz continuous gradient if there is some constant $L > 0$ such that
\begin{aligned} \|\nabla f(x) - \nabla f(y)\| \leq L \|x - y\| \end{aligned}
for any $x, y \in \mathbb{R}^d$. $L$ is called the Lipschitz constant. Note that $\|\cdot\|$ is the Euclidean norm.
We want to solve the problem
\begin{aligned} \min_{x \in \mathbb{R}^d} f(x) \end{aligned}
where $f : \mathbb{R}^d \rightarrow \mathbb{R}$ is a differentiable convex function with Lipschitz continuous gradient. To prove the convergence of gradient descent to the global minimum $x^*$, we need the following facts.
Proposition 3. (Three-point identity) For any points $a, b, c \in \mathbb{R}^d$,
\begin{aligned} \langle b - a, c - b \rangle = \frac{1}{2} \|c - a\|^2 - \frac{1}{2} \|b - a\|^2 - \frac{1}{2} \|c - b\|^2. \end{aligned}
Proof. Just expand and simplify the right-hand side. $\blacksquare$
Lemma 4. (Descent Lemma) For any points $x, y \in \mathbb{R}^d$,
\begin{aligned} f(x) \leq f(y) + \langle \nabla f(y), x - y \rangle + \frac{L}{2} \|x - y\|^2. \end{aligned}
Proof. Define $g(\tau) = f(y + \tau(x - y))$. By the fundamental theorem of calculus,
\begin{aligned} f(x) - f(y) = g(1) - g(0) = \int_0^1 g’(\tau) \, d\tau = \int_0^1 \langle \nabla f(y + \tau(x - y)), x - y \rangle \, d\tau. \end{aligned}
It follows that
\begin{aligned} f(x) - f(y) - \langle \nabla f(y), x - y \rangle &= \int_0^1 \langle \nabla f(y + \tau(x - y)) - \nabla f(y), x - y \rangle \, d\tau \\ &\leq \int_0^1 |\langle \nabla f(y + \tau(x - y)) - \nabla f(y), x - y \rangle| \, d\tau \\ &\leq \|x - y\| \int_0^1 \|\nabla f(y + \tau(x - y)) - \nabla f(y)\| \, d\tau \\ &\leq \|x - y\| \int_0^1 L\|\tau(x - y)\| \, d\tau \\ &= \frac{L}{2} \|x - y\|^2. \end{aligned}
We have used the Cauchy-Schwarz inequality at the third line and Lipschitz continuity of $\nabla f(x)$ at the fourth line. This proves the lemma. $\blacksquare$
Lemma 5. Given $z \in \mathbb{R}^d$, define
\begin{aligned} z^+ = z - \frac{1}{L} \nabla f(z). \end{aligned}
We then have
\begin{align} f(z^+) - f(x) &\leq L \langle z - x, z - z^+ \rangle - \frac{L}{2} \|z^+ - z\|^2 \\ &= \frac{L}{2} \|z - x\|^2 - \frac{L}{2} \|z^+ - x\|^2. \end{align}
Proof. We have
\begin{aligned} f(x) &\geq f(z) + \langle x - z, \nabla f(z) \rangle, \\ f(z^+) &\leq f(z) + \langle z^+ - z, \nabla f(z) \rangle + \frac{L}{2} \|z^+ - z\|^2. \end{aligned}
The first inequality is the definition of convexity, and the second inequality is the descent lemma. Subtract the first inequality from the second inequality to obtain
\begin{aligned} f(z^+) - f(x) &\leq \langle z^+ - x, \nabla f(z) \rangle + \frac{L}{2} \|z^+ - z\|^2 \\ &= L \langle z^+ - x, z - z^+ \rangle + \frac{L}{2} \|z^+ - z\|^2 \\ &= L \langle z - x, z - z^+ \rangle - \frac{L}{2} \|z^+ - z\|^2 \\ &= \frac{L}{2} \|z - x\|^2 - \frac{L}{2} \|z^+ - x\|^2. \end{aligned}
The last equality follows from the three-point identity. $\blacksquare$
Gradient Descent
Let us now analyze the convergence of gradient descent:
\begin{aligned} x_{k + 1} = x_k - \frac{1}{L} \nabla f(x_k). \end{aligned}
Putting $x = x^*$, $z = x_k$ and $z^+ = x_{k + 1}$ in (2) yields
\begin{align} f(x_{k + 1}) - f(x^*) \leq \frac{L}{2}( \|x_k - x^*\|^2 - \|x_{k + 1} - x^*\|^2 ). \end{align}
Putting $x = x_k$, $z = x_k$ and $z^+ = x_{k + 1}$ in (2) yields
\begin{align} f(x_{k + 1}) - f(x_k) \leq -\frac{L}{2} \|x_{k + 1} - x_k\|^2 \leq 0. \end{align}
Sum both sides of (3) from $k = 0$ to $n - 1$ to obtain
\begin{aligned} \sum_{k = 0}^{n - 1} f(x_{k + 1}) - n f(x^*) \leq \frac{L}{2}(\|x_0 - x^*\|^2 - \|x_n - x^*\|^2) \leq \frac{L}{2} \|x_0 - x^*\|^2. \end{aligned}
Observe that
\begin{aligned} nf(x_n) - \sum_{k = 0}^{n - 1} f(x_{k + 1}) &= \sum_{k = 0}^{n - 1} { (k + 1) f(x_{k + 1}) - k f(x_k) } - \sum_{k = 0}^{n - 1} f(x_{k + 1}) \\ &= \sum_{k = 0}^{n - 1} k(f(x_{k + 1}) - f(x_k)) \leq 0 \end{aligned}
by (4). It follows that
\begin{aligned} f(x_n) - f(x^*) \leq \frac{L\|x_0 - x^*\|^2}{2n}. \end{aligned}
Accelerated Gradient Descent
We now show that we can improve the convergence rate by adding a momentum step:
\begin{aligned} x_k &= y_k - \frac{1}{L} \nabla f(y_k), \\ y_{k + 1} &= x_k + \theta_k (x_k - x_{k - 1}). \end{aligned}
Let $x = x_k$, $z = y_{k + 1}$, and $z^+ = x_{k + 1}$ in (1) to obtain
\begin{aligned} 2L^{-1} (f(x_{k + 1}) - f(x_k)) \leq 2 \langle y_{k + 1} - x_k, y_{k + 1} - x_{k + 1} \rangle - \|x_{k + 1} - y_{k + 1}\|^2. \end{aligned}
Let $x = x^*$, $z = y_{k + 1}$, and $z^+ = x_{k + 1}$ in (1) to obtain
\begin{aligned} 2L^{-1} (f(x_{k + 1}) - f(x^*)) \leq 2 \langle y_{k + 1} - x^*, y_{k + 1} - x_{k + 1} \rangle - \|x_{k + 1} - y_{k + 1}\|^2. \end{aligned}
Let us define
\begin{aligned} \Delta_k = f(x_k) - f(x^*) \end{aligned}
such that the above inequalities simplify to
\begin{align} 2L^{-1}(\Delta_{k + 1} - \Delta_k) &\leq 2 \langle y_{k + 1} - x_k, y_{k + 1} - x_{k + 1} \rangle - \|x_{k + 1} - y_{k + 1}\|^2, \\ 2L^{-1} \Delta_{k + 1} &\leq 2 \langle y_{k + 1} - x^*, y_{k + 1} - x_{k + 1} \rangle - \|x_{k + 1} - y_{k + 1}\|^2. \end{align}
Let $\{t_k\}_{k = 1}^\infty$ be some sequence of numbers greater than or equal to 1. Multiply (5) by $t_{k + 1} - 1$ and add (6) to obtain
\begin{aligned} & 2L^{-1} \{t_{k + 1} \Delta_{k + 1} - (t_{k + 1} - 1) \Delta_k\} \\ & \leq 2 \langle t_{k + 1} y_{k + 1} - (t_{k + 1} - 1)x_k - x^*, y_{k + 1} - x_{k + 1} \rangle - t_{k + 1} \|x_{k + 1} - y_{k + 1}\|^2. \end{aligned}
Multiplying the above inequality by $t_{k + 1}$ produces
\begin{aligned} & 2L^{-1} \{t_{k + 1}^2 \Delta_{k + 1} - (t_{k + 1}^2 - t_{k + 1}) \Delta_k\} \\ & \leq 2 \langle t_{k + 1} y_{k + 1} - (t_{k + 1} - 1)x_k - x^*, t_{k + 1}y_{k + 1} - t_{k + 1}x_{k + 1} \rangle - \|t_{k + 1}x_{k + 1} - t_{k + 1}y_{k + 1}\|^2 \\ & = \|t_{k + 1} y_{k + 1} - (t_{k + 1} - 1)x_k - x^*\|^2 - \|t_{k + 1}x_{k + 1} - (t_{k + 1} - 1)x_k - x^*\|^2. \end{aligned}
The last equality uses the three-point identity. Let us assume $t_{k + 1}^2 - t_{k + 1} \leq t_k^2$ such that the above inequality becomes
\begin{aligned} 2L^{-1} (t_{k + 1}^2 \Delta_{k + 1} - t_k^2 \Delta_k) \leq \|t_{k + 1} y_{k + 1} - (t_{k + 1} - 1)x_k - x^*\|^2 - \|t_{k + 1}x_{k + 1} - (t_{k + 1} - 1)x_k - x^*\|^2. \end{aligned}
Also, to obtain an inductive inequality (to understand what an “inductive inequality” is, look at inequality (7)), we want to have
\begin{aligned} t_{k + 1} y_{k + 1} - (t_{k + 1} - 1)x_k - x^* = t_k x_k - (t_k - 1)x_{k - 1} - x^* \end{aligned}
or equivalently,
\begin{aligned} y_{k + 1} = x_k + \left( \frac{t_k - 1}{t_{k + 1}} \right) (x_k - x_{k - 1}). \end{aligned}
Hence, we set $\theta_k = (t_k - 1) / t_{k + 1}$.
It follows that
\begin{aligned} 2L^{-1} (t_{k + 1}^2 \Delta_{k + 1} - t_k^2 \Delta_k) \leq \|t_k x_k - (t_k - 1)x_{k - 1} - x^*\|^2 - \|t_{k + 1}x_{k + 1} - (t_{k + 1} - 1)x_k - x^*\|^2 \end{aligned}
and so
\begin{align} 2L^{-1} t_{k + 1}^2 \Delta_{k + 1} + \|t_{k + 1}x_{k + 1} - (t_{k + 1} - 1)x_k - x^*\|^2 \leq 2L^{-1} t_k^2 \Delta_k + \|t_k x_k - (t_k - 1)x_{k - 1} - x^*\|^2 \end{align}
which implies (with $k = n - 1$)
\begin{aligned} 2L^{-1} t_n^2 \Delta_n &\leq 2L^{-1} t_n^2 \Delta_n + \|t_n x_n - (t_n - 1)x_n - x^*\|^2 \\ &\leq 2L^{-1} t_{n - 1}^2 \Delta_{n - 1} + \|t_{n - 1} x_{n - 1} - (t_{n - 1} - 1)x_{n - 2} - x^*\|^2 \\ &\leq 2L^{-1} t_{n - 2}^2 \Delta_{n - 2} + \|t_{n - 2} x_{n - 2} - (t_{n - 2} - 1)x_{n - 3} - x^*\|^2 \\ &\leq \cdots \\ &\leq 2L^{-1} t_1^2 \Delta_1 + \|t_1 x_1 - (t_1 - 1)x_0 - x^*\|^2. \end{aligned}
We assume $t_1 = 1$ such that
\begin{aligned} 2L^{-1} t_n^2 (f(x_n) - f(x^*)) = 2L^{-1} t_n^2 \Delta_n &\leq 2L^{-1} \Delta_1 + \|x_1 - x^*\|^2 \\ &= 2L^{-1}(f(x_1) - f(x^*)) + \|x_1 - x^*\|^2 \\ &= 2L^{-1} ( f(x_1) - f(x^*) + \frac{L}{2} \|x_1 - x^*\|^2 ) \\ &\leq \|x_0 - x^*\|^2. \end{aligned}
The last inequality follows from (2) with $x = x^*$, $z = x_0$, and $z^+ = x_1$. Thus,
\begin{aligned} f(x_n) - f(x^*) \leq \frac{L \|x_0 - x^*\|^2}{2 t_n^2}. \end{aligned}
Now, let us recall the assumptions on the sequence $\{t_k\}_{k = 1}^\infty$:
- $t_k \geq 1$,
- $t_1 = 1$,
- $t_{k + 1}^2 - t_{k + 1} \leq t_k^2$.
Solving $t_{k + 1}^2 - t_{k + 1} = t_k^2$ produces
\begin{aligned} t_{k + 1} = \frac{1 + \sqrt{1 + 4t_k^2}}{2} \geq t_k + \frac{1}{2} \end{aligned}
which implies that
\begin{aligned} t_k \geq t_1 + \frac{k - 1}{2} = 1 + \frac{k - 1}{2} = \frac{k + 1}{2} \geq 1. \end{aligned}
Hence, we conclude that the algorithm
\begin{aligned} x_k &= y_k - \frac{1}{L} \nabla f(y_k), \\ t_{k + 1} &= \frac{1 + \sqrt{1 + 4t_k^2}}{2}, \\ y_{k + 1} &= x_k + \left( \frac{t_k - 1}{t_{k + 1}} \right) (x_k - x_{k - 1}) \end{aligned}
has the improved convergence rate
\begin{aligned} f(x_n) - f(x^*) \leq \frac{2 L \|x_0 - x^*\|^2}{(n + 1)^2}. \end{aligned}
Because this algorithm has a faster rate of convergence, it is often called accelerated gradient descent.
Experiment
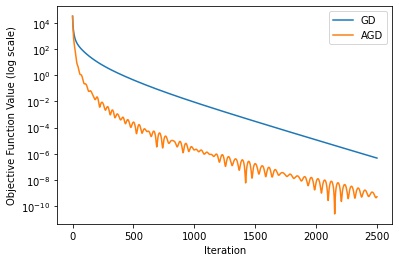
To see that adding an extrapolation step improves convergence, we compare the two algorithms on the problem
\begin{aligned} \min_{x \in \mathbb{R}^d} \frac{1}{2} \|Ax - b\|^2 \end{aligned}
where $A \in \mathbb{R}^{d \times d’}$ and $b \in \mathbb{R}^{d’}$. Note that since
\begin{aligned} \nabla \frac{1}{2} \|Ax - b\|^2 - \nabla \frac{1}{2} \|Ay - b\|^2 = A^\top (Ax - b) - A^\top (Ay - b) = A^\top A (x - y), \end{aligned}
the Lipschitz constant of this problem is the squared maximum singular value of $A$.
The below figure shows the result. Gradient descent is labeled “GD”, and accelerated gradient descent is labeled “AGD”. Indeed, AGD outperforms GD by a large margin.